Análisis. Límites de funciones. Continuidad

Ejercicios de límites de funciones
Ejercicios de continuidad de funciones
Ejercicios para practicar el cálculo de asíntotas


Aquí tienes las soluciones de los ejercicios del tema 8 de tu libro de texto

Examen de la 2ª Evaluación de Matemáticas I

Examen de la 2ª Evaluación

Examen de la 2ª Evaluación de 4º ESO

Examen de la 2ª Evaluación

Álgebra

Examen de la 2ª Evaluación

Examen de la 2ª Evaluación 2ºESO

Examen de la 2ª Evalución

Figuras planas

En el siguiente enlace podrás acceder al trabajo realizado por los alumnos para exponer en clase: Presentación de Figuras Planas

La geometría nos rodea
Quizás no te hayas parado nunca a pensar o no hayas observado como estamos rodeados en nuestra vida diaria de figuras circulares y de polígonos.

Polígonos
Los polígonos son figuras geométricas del plano limitadas por una línea poligonal cerrada.

Podemos clasificar los polígonos de diferentes formas. Para conocer más sobre los elementos de un polígono, las formas, su clasificación, etc puedes ver el enlace que anterior
Ejercicios. Polígonos

El teorema de Pitágoras

En primer lugar deberíamos recordar un par de ideas:
  
• Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir de 90º.
• En un triángulo rectángulo, el lado más grande recibe el nombre de hipotenusa y los otros dos lados se llaman catetos.

Teorema de Pitágoras.- En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Demostración: 

Quizás lo vea más fácil si miras en el dibujo siguiente:

Observa como se comprueba el Teorema de Pitágoras en el siguiente video 

 

Ejercicios para practicar el Teorema de Pitágoras

Áreas y perímetros de figuras planas

Ejercicios de áreas de figuras planas

Recuerda que en cualquier polígono, el perímetro es la suma de todos sus lados

Más ejercicios para que practiques el cálculo de áreas y perímetros de figuras planas

Soluciones a los ejercicios de tu libro de texto

Ejercicios para consolidar el tema._  Soluciones

Teorema de Thales

Anteriormente en Mati, una profesora muy particular

–¡Wow! –Sal estaba emocionado.

–Alucinante… –dijo Ven con los ojos brillantes.

–Lo es –admitió ella –Y todo gracias a un  Teorema de Tales.

–¿Qué es el teorema de Tales, Mati? –quiso saber Sal.

–Os lo cuento el próximo día –dijo ella –Y os enseñaré también más cositas con regla y compás.

–Vaya, parece que Mati hoy viene más tarde, Sal.

–¿Tienes tu regla y tu compás, Ven?

–Sí, claro –respondió el pequeño y añadió ilusionado –A ver  qué nos enseña hoy…

–El teorema de Tales, creo  –dijo el gafotas –Pero no estoy muy seguro de si se dice así…

–Pues sí, Sal –Mati acababa de llegar –Lo has dicho perfectamente, un teorema de Tales.

–¡Hola, Mati! –dijeron al unísono Sal y Ven, mientras Gauss se acercaba a las piernas de la recién llegada.

–¿Nos lo cuentas? –pidió Sal apresurado.

–Claro –respondió ella –Os contaré uno de los 2 teoremas de Tales.

–¿Sólo uno? –protestó Ven.

–Hoy uno –dijo la pelirroja –y otro día otro, ¿vale?

–Vale –terminó aceptando Ven.

–El teorema de Tales sobre triángulos semejantes–comenzó diciendo Mati –nos asegura que si dos rectas cualesquieras se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.

–¿Qué son triángulos semejantes, Mati? ¿Que se parecen mucho?

–Más o menos, Ven –respondió Mati —Dos triángulos son semejantes si tienen los tres ángulos iguales.

–¡Ajá! –exclamó Ven–Entonces son exactamente iguales.

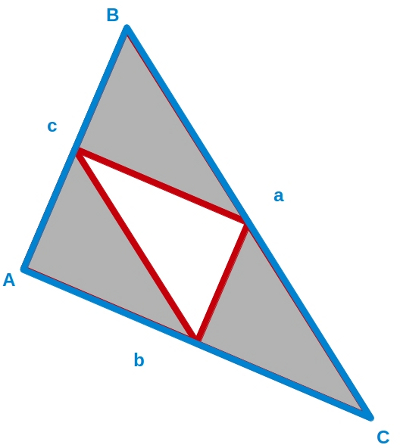
–No, Ven –le corrgió Mati –Pueden tener los mismos ángulos y ser de diferentes tamaños, mira:

–Estos 2 triángulos –continuó Mati –Tienen los 3 ángulos iguales y uno es mayor que el otro, ¿no?

–Imposible que tengan los mismos ángulos… –dijo Ven desconfiado.

–Ya verás –respondió ella –Podemos poner el ángulo A’ sobre A, el B’ sobre B y C’sobre C, y coinciden.

–¡Toma! Es verdad –terminó aceptando el pequeño.

–Pues bien, como os decía, el teorema de Tales nos asegura que si dos rectas cualesquieras se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra. Vamos a verlo con un dibujo: dibujamos estas 3 rectas rojas paralelas y dos rectas negras que la cortan.

–Por el teorema de Tales, lo que sabemos es que si dividimos la longitud del segmento AB entre la longitud del segmento A’B’, obtendremos el mismo valor que al dividir la de BC entre B’C’ y que al dividir la del segmento AC entre la del A’C’.

–Y eso, ¿qué tiene que ver con triángulos semejantes? –preguntó Sal arrugando su naricilla.

–Si aplicamos este teorema a triángulos semejantes como los 2 que hemos visto antes –dijo Mati — Lo que tenemos es que los lados son proporcionales.

–Ya veo… –murmuró el gafotas.

–Y yo… –dijo Ven, aunque no parecía muy convencido.

–Por eso –continuó ella –cuando el otro día teníamos esta construcción

–…teníamos dos triángulos semejantes, unidos en el punto A –les dijo –Y el  resultado de dividir el lado verde, de longitud 8, entre la de el lado azul, de longitud 4, en el mayor de los dos triángulos, es igual al resultado de dividir el segmento AB entre el lado de longitud 1  en el menor de los dos triángulos.

–¡Toma, toma, toma! ¡Cómo mola! –dijo Ven.

–Ah, claro… –se asombró Sal.

–Además –les propuso la pelirroja –os propongo un pequeño truco  para que podáis explicar el Teorema de Tales a vuestros amiguitos…

–¡Venga! –interrumpió Ven.

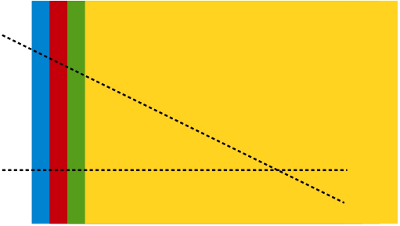
–Necesitamos 4 hojas de colores –les dijo –Y las colocamos así

–Ahora –continuó –las cortamos según dos líneas, con la dirección que queramos…

–Si separamos las hojas –les dijo Mati –tendremos 4 triángulos diferentes, le ponemos nombre a sus ángulos.

–Sabemos que los ángulos marcado con las letra B1, B2, B3 y B4 son iguales porque estaban unidos por ahí, ¿no? –les preguntó.

Los niños asintieron con la cabeza.

–Pues bien, pedidle a vuestros amigos que pongan los triángulos uno encima de otro pegados por los ángulos A1, A2, A3 y A4 , ya veréis…

–¡Claro! ¡Son semejantes! –dijo Sal.

–Sí –corroboró la pelirroja –Y si los pegáis por los ángulos C1, C2, C3 y C4 , también.

–¡Cómo mola, Mati! –Sal estaba entusiasmado.

–Voy a buscar cartulina de colores –dijo Ven.

–Estupendo –añadió Mati –Otro día seguiremos hablando de Tales…

de Blogs.20minutos.es 

Ejercicios para trabajar el teorema de Thales

ESCALAS Y PLANOS

Ejercicios sobre escalas y planos

Soluciones a los ejercicios de tu libro de texto

Si pinchas sobre el enlace que se muestra a continuación podrás acceder a la presentación realizada por los alumnos.

Presentación de Proporcionalidad. Teorema de Thales y escalas

Geometría

Aquí tienes algunos ejercicios más para practicar la geometría analítica de la recta
Y éstos para practicar la parte relativa a la circunferencia

Álgebra: Ecuaciones de primer grado

Aquí tienes más ecuaciones de primer grado para practicar, con sus correspondientes soluciones

Álgebra: Ecuaciones de segundo grado

Para que puedas practicar un poco más la resolución de ecuaciones de segundo grado, aquí te dejo un enlace en el que aparecen ecuaciones de segundo grado; una vez resueltas podrás comprobar si loo has hecho bien o no si haces click en SOLUCIÓN

Geometría: Examen

Examen de Geometría Analítica.   Solución

Trigonometría: Examen

Examen de Trigonometría

Examen de Álgebra

Aquí tienes el examen de álgebra que hemos realizado para que una vez has visto tu errores puedas rectificarlos

Álgebra: Exámen

Examen de Álgebra