Primitiva. Integral Indefinida

Ejercicios de Selectividad relativos a Integral Indefinida

Examen de 1ª Evaluación de Matemáticas Aplicadas

Examen de 1ª Evaluación de Matemáticas Aplicadas

Examen global de la 1ª evaluación

Examen global de la 1ª evaluación

Examen de Análisis

Os dejo aquí el examen de la primera evaluación 

Análisis

Aquí os dejo más ejercicios de Análisis variados para practicar más para el examen del martes. Soluciones

¡¡Ánimo!!

Examen de Trigonometría

Examen de Trigonometría

Potencias y raíces

Examen de potencias, notación científica y radicales (Matemáticas Aplicadas)

Examen de Análisis

En el siguiente enlace tenéis el enunciado del último examen de análisis que hicimos

Potencias y raíces

Examen de potencias y notación científica

Integral indefinida

Ejercicios de integrales indefinidas.   Soluciones


Aquí tienes más ejercicios de integrales, con éstos podrás practicar los distintos métodos que hemos trabajado en clase.    Soluciones

Aquí tienes el solucionario de la unidad correspondiente de tu libro de texto

Trigonometría

Para que puedas comprobar si has realizado bien los ejercicios de la unidad correspondiente de tu libro de texto, te dejo  aquí las soluciones. No las mires antes de intentarlo;  si no, no valdrá de nada.

Análisis

Aquí tenéis más ejercicios para trabajar la parte que llevamos vista de Análisis

Ejercicios varios de Análisis. Soluciones

Examen de Análisis

En el siguiente enlace tenéis el examen realizado de la primera parte de Análisis
Examen de Análisis

Análisis: Representación gráfica de funciones

Ejercicios de Representación gráfica de funciones. Soluciones de los ejercicios de representación gráfica

Aquí tienes las soluciones de los ejercicios correspondientes a la unidad de tu libro de texto

Números:Operaciones con Fracciones y Potencias

Examen de operaciones con fracciones y potencias

Álgebra

En esta unidad repasaremos la  resolución de los distintos tipos de ecuaciones:

• De primer grado
• De segundo grado
• Bicuadradas
• De grado superior a dos
• Racionales
• Irracionales
• Logarítmicas
• Exponenciales

Además recordaremos como resolver sistemas de ecuaciones lineales y no lineales

Para resolver sistemas de ecuaciones lineales de más de dos incógnitas, utilizaremos un nuevo método: El método de Gauss, que no es más que el método de reducción, que ya conocéis, pero aplicado de manera reiterada y de forma ordenada.

También recordaremos como resolver los distintos tipos de inecuaciones  y los sistemas de incubaciones con una incógnita.

Para que puedas practicar más, aquí tenéis:

Ejercicios de ecuaciones Logarítmicas y Exponenciales

Problemas

Más problemas
Soluciones1,   2,    3,    4

Aquí os dejo las Soluciones de los ejercicios de la unidad correspondiente de vuestro libro de texto, para que una vez los hayáis realizado podáis comprobar si vuestras soluciones son correctas

Ejercicios de Análisis

Para que puedas practicar un poco más, en estos enlaces os dejo más ejercicios de selectividad de algunos temas de Análisis. Soluciones
Ejercicios de extremos relativos y rectas tangentes . Soluciones

Fracciones y decimales

Examen de fracciones

Problemas de optimización

Relación de problemas de optimización de selectividad

Derivadas

Funciones derivadas

Ejercicios de derivadas de funciones. Soluciones de los ejercicios de cálculo de derivadas

Ejercicios de derivabilidad

Límites de funciones. Continuidad

Ejercicios de límites

Ejercicios  de continuidad

Para que una vez realizados los ejercicios de la unidad correspondiente de tu libro te texto podáis comprobar los resultados, os dejo aquí el solucionado de la unidad 1

Números reales

En este tema hacemos un breve repaso de los contenidos de 4º ESO

Para que podáis practicar un poco más de lo que hemos hecho en clase os dejo aquí algunas hojas de ejercicios. Sólo tenéis que picar en el enlace

Ejercicios de radicales
Ejercicios de logaritmos

Debes trabajar todos los ejercicios que necesites de tu libro de texto. Puedes comprobar las soluciones si haces click en el enlace que sigue Solucionario de la unidad 1 de tu libro de texto

Números complejos

Aquí tienes las soluciones de los ejercicios del tema correspondiente de tu libro de texto

Examen de Análisis

Examen de Análisis

Probabilidad

Aquí tienes las soluciones de los ejercicios del la unidad correspondiente de tu libro de texto para que puedas comprobar como los has realizado

Examen de Combinatoria

Examen de Combinatoria

Funciones. Representación gráfica

Soluciones de los ejercicios del tema 10 de tu libro de texto

Álgebra

Examen de ecuaciones, sistemas y problemas

Funciones

Examen de funciones
Examen de geometría y funciones

Geometría

Examen de Geometría

Combinatoria

Aquí tienes las soluciones de los ejercicios de tu libro de texto para que puedas comprobar si los has trabajado correctamente

Funciones

Examen de funciones

Sistemas de ecuaciones lineales con dos incógnitas

Aquí tienes las soluciones de los ejercicios relativos al tema de sistemas de ecuaciones de tu libro de texto

Examen de ecuaciones

Examen de ecuaciones 

Derivadas

Interpretación geométrica de la derivada en un punto
Funciones derivadas
Ejercicios de derivadas


Si haces click aquí encontraras las soluciones de los ejercicios de la unidad 9 de tu libro de texto

Ecuaciones

Para que puedas comprobar si has trabajado bien los ejercicios de tu libro de texto aquí tienes las soluciones de los ejercicios de la unidad de ecuaciones

En los siguientes enlaces encontrarás más ejercicios para practicar
Ejercicios de ecuaciones de primer grado. Soluciones
Ejercicios de ecuaciones de segundo grado. Soluciones
Problemas de ecuaciones. Soluciones

Funciones

Aquí tienes las soluciones de los ejercicios del tema de funciones de tu libro de texto para que puedas comprobar si los has trabajado de manera adecuada
Dominios. Puntos de corte. Continuidad. Soluciones
Continuidad y monotonía. Soluciones
Operaciones con funciones. Soluciones



Funciones elementales:
Soluciones de los ejercicios del tema correspondiente de tu libro de texto
Funciones polinómicas. Soluciones1. Soluciones2
Funciones racionales. Soluciones
Funciones exponenciales y logarítmicas. Soluciones1. Soluciones2

Análisis. Límites de funciones. Continuidad

Ejercicios de límites de funciones
Ejercicios de continuidad de funciones
Ejercicios para practicar el cálculo de asíntotas


Aquí tienes las soluciones de los ejercicios del tema 8 de tu libro de texto

Examen de la 2ª Evaluación de Matemáticas I

Examen de la 2ª Evaluación

Examen de la 2ª Evaluación de 4º ESO

Examen de la 2ª Evaluación

Álgebra

Examen de la 2ª Evaluación

Examen de la 2ª Evaluación 2ºESO

Examen de la 2ª Evalución

Figuras planas

En el siguiente enlace podrás acceder al trabajo realizado por los alumnos para exponer en clase: Presentación de Figuras Planas

La geometría nos rodea
Quizás no te hayas parado nunca a pensar o no hayas observado como estamos rodeados en nuestra vida diaria de figuras circulares y de polígonos.

Polígonos
Los polígonos son figuras geométricas del plano limitadas por una línea poligonal cerrada.

Podemos clasificar los polígonos de diferentes formas. Para conocer más sobre los elementos de un polígono, las formas, su clasificación, etc puedes ver el enlace que anterior
Ejercicios. Polígonos

El teorema de Pitágoras

En primer lugar deberíamos recordar un par de ideas:
  
• Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir de 90º.
• En un triángulo rectángulo, el lado más grande recibe el nombre de hipotenusa y los otros dos lados se llaman catetos.

Teorema de Pitágoras.- En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Demostración: 

Quizás lo vea más fácil si miras en el dibujo siguiente:

Observa como se comprueba el Teorema de Pitágoras en el siguiente video 

 

Ejercicios para practicar el Teorema de Pitágoras

Áreas y perímetros de figuras planas

Ejercicios de áreas de figuras planas

Recuerda que en cualquier polígono, el perímetro es la suma de todos sus lados

Más ejercicios para que practiques el cálculo de áreas y perímetros de figuras planas

Soluciones a los ejercicios de tu libro de texto

Ejercicios para consolidar el tema._  Soluciones

Teorema de Thales

Anteriormente en Mati, una profesora muy particular

–¡Wow! –Sal estaba emocionado.

–Alucinante… –dijo Ven con los ojos brillantes.

–Lo es –admitió ella –Y todo gracias a un  Teorema de Tales.

–¿Qué es el teorema de Tales, Mati? –quiso saber Sal.

–Os lo cuento el próximo día –dijo ella –Y os enseñaré también más cositas con regla y compás.

–Vaya, parece que Mati hoy viene más tarde, Sal.

–¿Tienes tu regla y tu compás, Ven?

–Sí, claro –respondió el pequeño y añadió ilusionado –A ver  qué nos enseña hoy…

–El teorema de Tales, creo  –dijo el gafotas –Pero no estoy muy seguro de si se dice así…

–Pues sí, Sal –Mati acababa de llegar –Lo has dicho perfectamente, un teorema de Tales.

–¡Hola, Mati! –dijeron al unísono Sal y Ven, mientras Gauss se acercaba a las piernas de la recién llegada.

–¿Nos lo cuentas? –pidió Sal apresurado.

–Claro –respondió ella –Os contaré uno de los 2 teoremas de Tales.

–¿Sólo uno? –protestó Ven.

–Hoy uno –dijo la pelirroja –y otro día otro, ¿vale?

–Vale –terminó aceptando Ven.

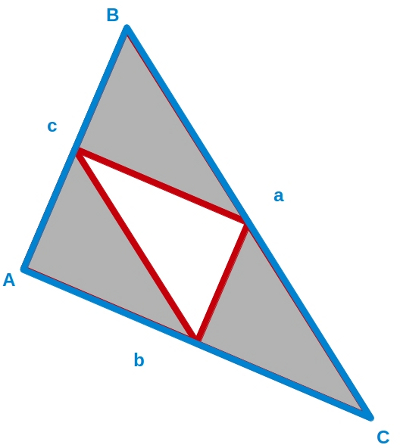
–El teorema de Tales sobre triángulos semejantes–comenzó diciendo Mati –nos asegura que si dos rectas cualesquieras se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.

–¿Qué son triángulos semejantes, Mati? ¿Que se parecen mucho?

–Más o menos, Ven –respondió Mati —Dos triángulos son semejantes si tienen los tres ángulos iguales.

–¡Ajá! –exclamó Ven–Entonces son exactamente iguales.

–No, Ven –le corrgió Mati –Pueden tener los mismos ángulos y ser de diferentes tamaños, mira:

–Estos 2 triángulos –continuó Mati –Tienen los 3 ángulos iguales y uno es mayor que el otro, ¿no?

–Imposible que tengan los mismos ángulos… –dijo Ven desconfiado.

–Ya verás –respondió ella –Podemos poner el ángulo A’ sobre A, el B’ sobre B y C’sobre C, y coinciden.

–¡Toma! Es verdad –terminó aceptando el pequeño.

–Pues bien, como os decía, el teorema de Tales nos asegura que si dos rectas cualesquieras se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra. Vamos a verlo con un dibujo: dibujamos estas 3 rectas rojas paralelas y dos rectas negras que la cortan.

–Por el teorema de Tales, lo que sabemos es que si dividimos la longitud del segmento AB entre la longitud del segmento A’B’, obtendremos el mismo valor que al dividir la de BC entre B’C’ y que al dividir la del segmento AC entre la del A’C’.

–Y eso, ¿qué tiene que ver con triángulos semejantes? –preguntó Sal arrugando su naricilla.

–Si aplicamos este teorema a triángulos semejantes como los 2 que hemos visto antes –dijo Mati — Lo que tenemos es que los lados son proporcionales.

–Ya veo… –murmuró el gafotas.

–Y yo… –dijo Ven, aunque no parecía muy convencido.

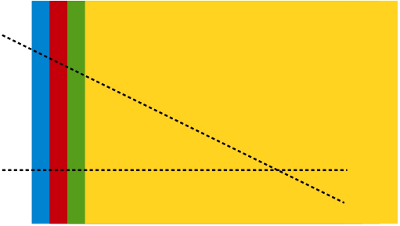
–Por eso –continuó ella –cuando el otro día teníamos esta construcción

–…teníamos dos triángulos semejantes, unidos en el punto A –les dijo –Y el  resultado de dividir el lado verde, de longitud 8, entre la de el lado azul, de longitud 4, en el mayor de los dos triángulos, es igual al resultado de dividir el segmento AB entre el lado de longitud 1  en el menor de los dos triángulos.

–¡Toma, toma, toma! ¡Cómo mola! –dijo Ven.

–Ah, claro… –se asombró Sal.

–Además –les propuso la pelirroja –os propongo un pequeño truco  para que podáis explicar el Teorema de Tales a vuestros amiguitos…

–¡Venga! –interrumpió Ven.

–Necesitamos 4 hojas de colores –les dijo –Y las colocamos así

–Ahora –continuó –las cortamos según dos líneas, con la dirección que queramos…

–Si separamos las hojas –les dijo Mati –tendremos 4 triángulos diferentes, le ponemos nombre a sus ángulos.

–Sabemos que los ángulos marcado con las letra B1, B2, B3 y B4 son iguales porque estaban unidos por ahí, ¿no? –les preguntó.

Los niños asintieron con la cabeza.

–Pues bien, pedidle a vuestros amigos que pongan los triángulos uno encima de otro pegados por los ángulos A1, A2, A3 y A4 , ya veréis…

–¡Claro! ¡Son semejantes! –dijo Sal.

–Sí –corroboró la pelirroja –Y si los pegáis por los ángulos C1, C2, C3 y C4 , también.

–¡Cómo mola, Mati! –Sal estaba entusiasmado.

–Voy a buscar cartulina de colores –dijo Ven.

–Estupendo –añadió Mati –Otro día seguiremos hablando de Tales…

de Blogs.20minutos.es 

Ejercicios para trabajar el teorema de Thales

ESCALAS Y PLANOS

Ejercicios sobre escalas y planos

Soluciones a los ejercicios de tu libro de texto

Si pinchas sobre el enlace que se muestra a continuación podrás acceder a la presentación realizada por los alumnos.

Presentación de Proporcionalidad. Teorema de Thales y escalas

Geometría

Aquí tienes algunos ejercicios más para practicar la geometría analítica de la recta
Y éstos para practicar la parte relativa a la circunferencia

Álgebra: Ecuaciones de primer grado

Aquí tienes más ecuaciones de primer grado para practicar, con sus correspondientes soluciones

Álgebra: Ecuaciones de segundo grado

Para que puedas practicar un poco más la resolución de ecuaciones de segundo grado, aquí te dejo un enlace en el que aparecen ecuaciones de segundo grado; una vez resueltas podrás comprobar si loo has hecho bien o no si haces click en SOLUCIÓN

Geometría: Examen

Examen de Geometría Analítica.   Solución

Trigonometría: Examen

Examen de Trigonometría

Examen de Álgebra

Aquí tienes el examen de álgebra que hemos realizado para que una vez has visto tu errores puedas rectificarlos

Álgebra: Exámen

Examen de Álgebra

Álgebra

Expresiones Algebraicas: Polinomios

Aquí tienes las soluciones del tema correspondiente de tu libro de texto

Ecuaciones 

Aquí encontrarás todas las soluciones de los ejercicios del tema de ecuaciones de tu libro de texto 

Progresiones Aritméticas y Geométricas

Progresiones Aritméticas

Algunos ejercicios de progresiones aritméticas para practicar

Progresiones Geométricas

Ejercicios de Progresiones Geométricas Ten en cuenta que para ver la solución de cada ejercicio tendrás que picar en la pestaña superior en el número de ejercicio para el que quieres conocer la solución

Soluciones a los ejercicios de tu libro de texto

PARA QUE SIRVEN LAS MATEMÁTICAS?

Lugares Geométricos: Cónicas

Resumen
 Esquema de Cónicas

Ejercicios de geometría: La circunferencia

Aquí tienes las soluciones de los ejercicios del tema correspondiente de tu libro de texto para que puedas comprobar si los has trabajado correctamente

Trigonometría y Semejanza de triángulos

Las 11 Aplicaciones de la Trigonometría más destacadas

Existen diversas aplicaciones de la trigonometría en la ciencia y en la vida cotidiana.

Sus aplicaciones más destacadas se muestran en la navegación, la geografía, la astronomía, la arquitectura y en todos los campos de la ingeniería. 

La utilización de la trigonometría en las ciencias y en la vida cotidiana se debe a que a través de esta se obtienen medidas precisas.

Las medidas se obtienen mediante el estudio de las relaciones existentes entre los lados de los triángulos con respecto a los ángulos. 

Para ello es necesario aplicar las funciones trigonométricas: seno, coseno, tangente, cotangente, secante y cosecante.

La trigonometría es la rama de las matemáticas que es necesaria tanto para el estudio geométrico como para el cálculo y el análisis matemático.

El uso de la trigonometría en las ciencias y en la vida cotidiana se remonta aproximadamente al año 4000 a. C.

De acuerdo con los datos históricos, el uso de la trigonometría inició en Babilonia y en Egipto, ya que para poder realizar sus construcciones fue necesario realizar grandes cálculos.

1- Aplicaciones en la astronomía 

La trigonometría se usa en la astronomía para calcular la distancia del planeta Tierra al Sol, a la Luna, el radio de la Tierra y también para medir la distancia entre los planetas.

Para realizar esas mediciones se valen de la triangulación, la cual consiste en tomar distintos puntos de lo que se desea medir y considerar cada uno como vértices de triángulos; de ahí se saca la distancia entre un punto y otro.

Los egipcios establecieron la medida de los ángulos en grados, minutos y segundos, y lo utilizaron en la astronomía.

2- Aplicaciones en la arquitectura

La aplicación de la trigonometría en la arquitectura es algo que nunca debe faltar. De su uso depende la creación de los planos y su posterior ejecución.

La creación de una casa o de un edificio debe seguir unos parámetros específicos. Por ejemplo: se debe medir cada ángulo de todas las paredes y las columnas con el objeto de evitar alguna deformidad que con el tiempo pueda hacer que el edificio se derrumbe.

Un ejemplo claro del uso de la trigonometría en la arquitectura se observa en las pirámides egipcias y en las construcciones realizadas por las civilizaciones que habitaban el continente americano antes de la llegada de los españoles.

Debido a la aplicación de la trigonometría es que esas construcciones siguen casi intactas con el paso del tiempo.

3- Aplicaciones en la navegación

La trigonometría fue utilizada en la navegación durante muchos años y para ello crearon lo que hoy se conoce como sextante, instrumento con el que se podía medir la distancia triangulando con el Sol o las estrellas.

El sextante era utilizado de la siguiente manera: se debía determinar la altura angular del Sol (o de las estrellas o de cualquier astro que pueda servir como punto de referencia) por encima del horizonte.

Posteriormente se podrían realizar cálculos matemáticos para determinar el punto en el que se encuentra el observador, es decir, la persona que está usando el sextante.

Conociendo dos puntos de una costa o una isla, el sextante también podía ser utilizado para medir la distancia en la que se encontraban los barcos de la costa.

El sextante era el encargado de orientar a los capitanes de los barcos. En la actualidad el sextante ha sido reemplazo por los sistemas satelitales. Estos también se valen del uso de la trigonometría.

4- Aplicaciones en la geografía

En la geografía la trigonometría se usa para el cálculo de las distancias en un mapa; es decir, se vale de los paralelos y los meridianos para poder calcular la longitud.

5- Aplicaciones en los videojuegos

La trigonometría se usa para la programación de videojuegos. Por esto, todo lo que se presenta en la pantalla requiere de la trigonometría.

6- Aplicaciones en la ingeniería civil

Un ejemplo del uso de la trigonometría en la ingeniería civil se observa mediante la construcción de puentes, carretera, edificios y en el trazo de levantamiento de terrenos, entre otros.

7- Aplicaciones en la ingeniería mecánica 

La trigonometría se usa en la ingeniería mecánica para el diseño y medición de piezas en series. También se usa para proyectar fuerzas.

8- Aplicaciones en la ingeniería electrónica

La trigonometría se usa en la ingeniería electrónica para identificar el comportamiento de series y de señales.

La trigonometría ayuda a establecer conexiones y ubicar posiciones que favorezcan el proceso de distribución de la energía eléctrica.

9- Aplicaciones en el billar

La trigonometría es aplicada en este juego de mesa. Con base en el choque entre las bolas, hace que cada una de vaya en una dirección en particular creando unos ángulos específicos. 

Estos ángulos son usados por cada jugador para determinar cuál será su siguiente movimiento.

10- Aplicaciones en la física

Para medir la trayectoria de un objeto se usa la trigonometría. Por ejemplo: cuando en un partido de fútbol se quiere hacer un pase aéreo es necesario buscar un ángulo y tener bien definido el punto hacia donde va dirigido.

Tomando en cuenta todos estos puntos se puede calcular la trayectoria del balón. Esto también puede ser aplicado para medir la trayectoria de un proyectil, un cohete, entre otros elementos.

11- Aplicaciones en la medicina

La trigonometría se aplica en la medicina para poder leer los electrocardiogramas, examen que registra gráficamente la actividad eléctrica del corazón en función del tiempo.

En estos estudios aparecen funciones del seno y el coseno. De acuerdo a cómo van apareciendo se les va otorgando una letra que le da significada a la onda. Esto permite que los médicos lo puedan leer y dar un diagnóstico oportuno.

Aquí tienes las soluciones de los ejercicios del tema correspondiente de tu libro de texto para que puedas realizar todos los que consideres oportuno y comprobar las soluciones

Estas son las soluciones del tema de Aplicaciones de la Trigonometría de tu libro de texto