Feliz Navidad

Feliz Navidad a todos!!!!

Examenes del primer trimestre

Para que puedas  trabajar los errores que cometiste y repasar un poco más para el examen de evaluación aquí tienes

Examen del bloque de números
Examen de parte del bloque de álgebra

Examen de fracciones y decimales

Aquí tenéis el examen de fracciones y decimales

Trigonometría: examen

Aquí tienes el examen de Trigonometría para que puedas trabajarlo tranquilamente en casa y rectificar los errores que hubieras tenido
Ésta es una posible forma de resolver el problema 5 (el del árbol)

Potencias y radicales

Aquí tienes el examen de potencias y radicales  para que puedas trabajarlo y rectificar los errores que cometiste

Álgebra. Ecuaciones y sistemas

ECUACIONES

Son igualdades entre dos expresiones algebraicas

Pueden ser:

• POLINÓMICAS: Son aquellas que se pueden escribir en la forma P(x) = 0 (P(x) es un polinomio). 
  Se resuelven de una manera u otra dependiendo del grado del polinomio
  • De primer grado 
    Para resolverlas puedes recordar los pasos a seguir aquí
  • De segundo grado
    Si es completa ax²+ bx + c = 0, aplicamos la fórmula 
    
    
    
    Si es incompleta

    ◊ de la forma ax²+ bx = 0, extraemos x factor común e igualamos a 0 cada factor

    
    
    ◊ de la forma ax²+ c = 0, despejamos x y no olvidamos poner el doble signo al extraer la raíz cuadrada
  • De grado tres o superior la resolvemos factorizando por Ruffini, las raices serán las soluciones de la ecuación
    3x⁴+ x³− 9x²− 9x− 2 = 0 
  • Bicuadradas: Hacemos el cambio de variable x²= z por ejemplo y resolvemos la ecuación resultante de 2º grado en z. Las soluciones de la primera serán las raíces positivas y negativas de z
    
    
    x⁴– 15x² - 16 = 0
• RACIONALES: Están formadas por fracciones algebraicas. Aparecen incógnitas en el denominador
  
  
  
  Una vez reduzcamos a común denominador (hallando el mínimo común múltiplo de los denominadores después de factorizar los polinomios), podremos eliminarlos (¡porque habremos multiplicado por la misma expresión en ambos miembros!!) y trabajaremos con una ecuación polinómica

No olvides comprobar las soluciones!!!!!

No siempre son válidas todas las que hallamos porque al multiplicar por la exprersión del denoominador para poder suprimirlos puede ser que estemos multiplicando por cero y en ese caso la ecuación obtenida no será equivalente a la anterior

• IRRACIONALES: Son aquellas en las que la incógnita aparece en el radicando de una raíz.
  
  
  

Para resolverlas debemos dejar la raiz sóla en un miembro y después elevar al cuadrado ambos miembros para que de esta forma desaparezca la raiz y nos quedemos con una ecuación polinómica.

Una vez resuelta es necesario comprobar si las soluciones son válidas porque al haber elevado al cuadrado podemos haber introducido soluciones no válidas

• EXPONENCIALES: Son aquellas en las que la incógnita aparece en el exponente

Para resolverlas se aplican las propiedades de las potencia

• O bien expresamos todas las potencias como potencias de la misma base, dejando una sóla en cada miembro para poder igualar los exponentes
  81^2x= 9
• Realizamos un cambio de variable (si aparecen sumas de potencias) para poder convertirla en una ecuación polinómica
  4^x+ 3 · 2^x+1− 16 = 0

• LOGARITMICAS: Son aquellas en las que la incógnita aparece formando parte de un logaritmo.
  Para resolverlas las transformaremos en ecuaciones polinómicas mediante la definición o las propiedades de los logaritmos.

2 logx−log(x+ 4) = log 2

Hay que comprobar las soluciones y descartar las que hagan negativo o nulo el argumento de un logaritmo porque no está definido

Ejercicios de repaso de ecuaciones

Aquí tienes la soluciones de los ejercicios de la unidad correspondiente de tu libro de texto para que puedas comprobar que los has trabajado de manera correcta
Para que puedas practicar más aquí tienes algunos ejercicios de

• Ecuaciones polinómicas. Soluciones
• Ecuaciones racionales e irracionales. Soluciones
• Ecuaciones exponenciales y logarítmicas. Soluciones

Trigonometría

Recuerda

Signo de las razones Trigonométricas en los distintos cuadrantes

  

Circunferencia Goniométrica. Razones

Recuerda que resolver un triángulo consiste en hallar todos sus lados y todos sus ángulos, para ello debes tener en cuenta:

• El Teorema de Pitágoras, si el triángulo es rectángulo
• Que la suma de todos los ángulos de un triángulo es 180º
• Los teoremas del seno y del coseno

Para que puedas comprobar si has trabajado bien los ejercicios de la unidad de tu libro de texto que no hayamos corregido en clase, aquí tienes las soluciones de todos los ejercicios de la unidad

Puedes trabajar un poco más con estos ejercicios para reforzar lo aprendido
Reducción de ángulos al primer cuadrante. Soluciones
Calculo de razones trigonométricas a partir de otras dadas. Soluciones
Ecuaciones Trigonométricas. Soluciones1, Soluciones2, Soluciones 3
Resolución de triángulos. Soluciones1, Soluciones2

Fracciones y Decimales

Para que puedas comprobar si has trabajado bien los ejercicios de la unidad 2 de tu libro de texto, si haces click aquí podrás ver las soluciones
Ejercicios de operaciones con fracciones. Soluciones
Ejercicios de números decimales, clasificación, fracción generatriz. Soluciones
Ejercicios para practicar el redondeo y el cálculo del error cometido al aproximar. Soluciones

Álgebra. Expresiones Algebraicas

Aquí os dejo algunos ejercicios para que podáis practicar más

Ejercicios de operaciones con polinomios. Soluciones
Cálculo de las raíces de un polinomio y factorización de polinomios. Soluciones
Ejercicios de operaciones con fracciones algebraicas. Soluciones

Comprueba si has realizado correctamente los ejercicios de tu libro de texto con el archivo que tienes aquí

Álgebra. Polinomios

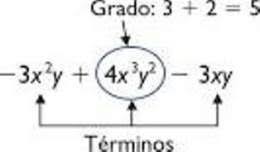
Recuerda la terminología para referirnos a las distintas partes de un polinomio

Observa que cuando hay más una variable en el polinomio el grado de cada término es la suma de los grados de cada variable

OPERACIONES CON POLINOMIOS

Suma de polinomios

Diferencia de polinomios

Ejercicios de suma de polinomios

Producto de polinomios

Ejercicios de producto de polinomios

División de polinomios

Para dividir un polinomio P(x) entre uno del tipo (x-a) es muy útil la regla de Ruffini

Ejercicios de aplicación de la regla de Ruffini

Ejercicios del teorema del resto

Factorización de polinomios

Recuerda que para factorizar polinomios puedes utilizar alguna o varias de las siguientes técnicas

• Extraer factor común
• Aplicar las identidades notables
• Hallando las raíces de la ecuación de 2º grado asociada al polinomio
• Dividiendo por Ruffini para hallar las raíces

No debes confundir

                                  Si a es una raíz del polinomio el factor correspondiente es x - a

Ejercicios de factorización de polinomios

Potencias y Radicales

Si haces click aquí  encontrarás más ejercicios con radicales para seguir practicando

Soluciones a los ejercicios de potencias y radicales de tu libro de texto

Radicales

RADICALES

Un radical no es más que una potencia en la que el exponente  es un número racional, tendremos

Para poder trabajar con radicales ten en cuenta:

Producto de radicales

No olvides que para poder multiplicar y dividir radicales deben de tener el mismo índice, si no fuera así tendrías que reducir a índice común

Suma de radicales

RECUERDA sólo podrás sumar aquellos radicales que sean semejantes

Aquí tienes un ejemplo de suma de radicales en los que no todos son semejantes. 

Observa

Ten en cuenta que puedes encontrar radicales que aunque a simple vista no te parezcan semejantes, una vez simplificados puedes comprobar que si lo son

Recuerda que para simplificar radicales puedes

• Extraer factores
• Una vez pasado a potencia de exponente fraccionario simplificar la fracción del exponente

Si haces click aquí podrás realizar algunos ejercicios de sumas con radicales

Ejercicios de productos de radicales

Potencias

POTENCIAS

Tabajamos ahora con potencias

Recuerda las propiedades de las potencias

Observa que tenemos propiedades para 

• multiplicar o dividir potencias de la misma base o 
• multiplicar o dividir potencias del mismo exponente

Practica con ellas realizando los ejercicios que aparecerán al picar aquí

Examen de Números, Ecuaciones y Sistemas

Aquí tienes el examen de números, ecuaciones y sistemas para que puedas trabajarlo tranquilamente en casa y así corregir los errores cometidos

Examen de decimales fracciones

Aquí tienes el examen de la unidad 1 para que puedas practicarlo tranquilamente en casa y corregir tus errores

Examen de números enteros

Aquí tienes el examen de números enteros para que puedas realizarlo tranquilamente en casa y corregir así tus errores

Números reales

Potencias. Notación científica
Recuerda las propiedades de las potencias

Ejercicios de potencias y notación científica. Soluciones

Radicales
    º

No son más que potencias de exponente fraccionario

Para operar con radicales debes recordar

No olvides que       sólo podrás sumar aquellos radicales que sea semejantes

Ejercicios con radicales. Soluciones

Logaritmos
Son la función inversa de la función exponencial

Ejercicios con logaritmos. Soluciones

Interés simple e interés compuesto

Ejercicios resueltos de interés simple y de interés compuesto

Para que puedas trabajar todos los ejercicios del tema y comprobar tus soluciones aquí tienes las soluciones de los ejercicios de la unidad 1 de tu libro de texto

Divisibilidad. Números enteros

Criterios de divisibilidad

Practica estos criterios con los ejercicios que encontrarás en el siguiente enlace
Ejercicios de divisibilidad
Soluciones a los ejercicios anteriores

Mínimo común múltiplo (m.c.m)
¿Qué es?
Es el menor de los múltiplos que tienen en común dos o más números
¿Cómo se calcula?
Para hallar el mínimo común múltiplo de dos o más números, una vez tengamos la descomposición factorial de dichos números, tomaremos los factores comunes y los factores no comunes elevados a su máximo exponente.

💥   ¡¡ Ten en cuenta que el número que obtengas debe ser mayor que los dados o al menos el mayor de todos !!

Máximo común divisor (m.c.d)
¿Qué es?
Es el mayor de los divisores que tienen en común dos o más números
¿Cómo se calcula?
Para hallar el máximo común divisor de dos o más números, una vez tengamos la descomposición factorial de dichos números, tomaremos los factores comunes elevados a su menor exponente.

💥 ¡¡ Ten en cuenta que el número que obtengas debe ser menor que los dados o al menos el menor de todos!!
Ejercicios de mcm y mcd. (Soluciones)

Operaciones con. números enteros
Para realizar  operaciones con números enteros debes tener en cuenta 

No debes confundir la regla de los signos para el producto con el resultado del signo en la suma de números enteros 

Ejercicios de operaciones con números enteros. Soluciones

Para que puedas trabajar todos los ejercicios de tu libro de texto te dejo aquí el enlace con las soluciones de la unidad 1 de tu libro de texto

Soluciones de los ejercicios del tema1 de tu libro de texto

Exámenes Finales de Recuperación de 3º ESO

Los exámenes finales y de recuperación se personalizaron según los distintos estándares por alcanzar por parte de los alumnos. Se incluyen en cada uno ejercicios relativos a los estándares por alcanzar y algunas ejercicios que pudieran mejorar.

A continuación, al hacer click en cada enlace, aparecerán los distintos modelos utilizados en uno de los grupos y el total de preguntas que se fueron combinando en el otro grupo.

Examen final de recuperación de 3º ESO-A.  Este modelo contiene todas las preguntas a combinar

Examen final de recuperación de 3º ESO-B(todo). Para los alumnos que tenían suspensas todas las evaluaciones

Examen final y de recuperación 3ºESO-B (1ª). Para los alumnos que tuvieran suspensos los estándares de la 1ª evaluación en su mayoría

Examen final y de recuperación 3ºESO-B (1ª y 2ª). Para aquellos alumnos con los estándares de la 1ª y de la 2ª evaluación por alcanzar

Examen final y de recuperación 3ºESO-B (2ª). Para los alumnos que tuvieran pendiente de alcanzar  los estándares de la 2ª evaluación.

Examen final y de recuperación 3ºESO-B (3ª). Para los alumnos que debieran  alcanzar  los estándares de la 3ª evaluación.

Examen final y de recuperación 3ºESO-B (1ª y 3ª). Para aquellos alumnos con los estándares de la 1ª y de la 3ª evaluación por alcanzar

Examen final y de recuperación 3ºESO-B (2ª y 3ª). Para aquellos alumnos con los estándares de la 2ª y de la 3ª evaluación por alcanzar

Exámenes de Geometría

Examen de Proporcionalidad: Teorema de Tales y Figuras semejantes. Figuras Planas

Exámen final

Examen final de Junio

Movimientos en el plano

Presentación realizada por los alumnos de 3ºA

Para que podais ver el enlace que aparece en la presentación sobre la simetría en la música os dejo aquí el video correspondiente

Soluciones a los ejercicios de la unidad correspondiente en tu libro de texto

Puedes practicar un poco más con estos ejercicios

Calcula coordenadas de vectores
Suma y resta vectores
Ficha1: Vectores. Traslaciones
Ficha2: Simetría Axial y Central
Ficha 3: Ejes y centros de simetrías de figuras planas
Soluciones a los ejercicios de las fichas anteriores

Ecuaciones

¿Para qué sirven las ecuaciones y cómo se resuelven?

Este esquema te puede ayudar a resolver ecuaciones

Ejercicios interactivos para practicar

Ejercicios de ecuaciones para practicar

Algunos más

EXAMEN

Examen de Geometría .- Solución: pag 1.- pag 2.- pag 3.- pag 4.- pag5.- pag 6.- pag7

MAGNITUDES PROPORCIONALES. PORCENTAJES

RAZÓN 
La razón entre dos números a y b es el cociente entre dichos números, 

• Se lee a es a b
• Una razón no tiene unidades. 
• Los números a y b pueden ser enteros o decimales.
• Ten en cuenta que una razón se escribe en forma de fracción pero no lo es; en una fracción el numerador y el denominador son números enteros y en la razón pueden ser decimales

EJEMPLO

Compramos 3 kg de cerezas por 6 €. Podemos establecer la relación entre el precio (6 €) y la cantidad (3 kg) 

6:3 = 2 € el kilo

 es la razón entre euros y cerezas.

PROPORCIÓN NUMÉRICA

Es una igualdad entre dos razones

Las proporciones cumplen la siguiente relación fundamental:

a·d = b·c

(El producto de los extremos es igual al producto de los medios)

EJEMPLO:

Los números 2, 5 y 8, 20 forman una proporción, ya que la razón entre 2 y 5 es la misma que la razón entre 8 y 20.

Es decir 

EJEMPLO:

En la tabla que sigue se observa que 


cada árbol da

La razón de proporcionalidad es 50.     

Con ese dato podemos completar la tabla para los siguientes casos.

Para hallar el número de árboles en el caso de haber recolectado 400 Kg de fruta

Así que 

Por lo tanto  x = 8

De la misma forma hallaremos el resto

Kg de fruta	200	400	100	50	500	150	3000	1000
Nº de árboles	4	8	2	1	10	3	60	20

EJERCICIOS:

1. Completa las siguientes proporciones: 

    a) b)c) 

 2.  Ordena estos datos para componer una proporción:

    a) 12, 3, 40, 10      b) 24, 40, 50, 30      c) 0,36; 0,06; 0,3; 1,8

 3. Completa la siguiente tabla sabiendo que la razón de proporción        es 4,5

PROPORCIONALIDAD DIRECTA

Dos magnitudes son directamente proporcionales si, al multiplicar una de ellas por un número, la otra queda multiplicada por el mismo número.

EJEMPLO

El número de personas que vienen a comer y la cantidad de comida que necesito. Por ejemplo si el número de personas es el triple habrá que preparar triple cantidad de comida. 

EJERCICIOS:

Indica si las siguientes magnitudes son directamente proporcionales o no:
a) La edad de una persona y su número de teléfono
b) El tamaño de un recipiente y el nº de litros que puede contener
c) Kilos de naranjas compradas y euros a pagar
e) Peso de una persona y número de libros que lee al año

REGLA DE TRES DIRECTA

Para resolver problemas de proporcionalidad directa, podemos utilizar el método de reducción a la unidad

EJEMPLO
Si por cinco paquetes de palomitas hemos pagado 3,50 € ¿Cuánto tendremos que pagar por tres paquetes? 

Primero calculamos el precio de un paquete.  3,50 : 5 = 0,70 €
Ahora podemos calcular el precio de los tres.  0,70 · 3 = 2,10€

La regla de tres es otro procedimiento para calcular el cuarto término de una proporción

En el ejemplo anterior de los paquetes de palomitas, podríamos ordenar los datos teniendo en cuenta la proporción:

Por lo tanto 

x= 2,10

La forma habitual de plantear la regla de tres es situando los datos de esta forma:

      5 paquetes-----------> 3,50€

3 paquetes----------->   x

Para hallar x multiplicamos en cruz y dividimos entre el tercer término

De donde obtenemos que x = 2,10

Practica con los ejercicios que aparecerán al hacer click aquí

PORCENTAJES

El porcentaje o tanto por ciento es la proporción directa más utilizada en nuestra vida diaria

En los comercios, informaciones periodísticas, o en los análisis de resultados de cualquier actividad aparecen porcentajes.

Un porcentaje es una razón en la que su denominador es 100
Su símbolo es %

Para calcular un tanto por ciento puedes

•  Aplicar una regla de tres, o 
•  Multiplicar por el tanto y dividir entre 100

EJEMPLO
Calcula el 21% de 700 

El 21% de 700 es 

Por lo tanto el 21% de 700 es 14,7

Practica con estos ejercicios

Para repasar

Examen de magnitudes proporcionales